二叉查找树已经实现了, 但是二叉查找树有个巨大的缺点, 即可能会出现不平衡的状态, 比如使用我们自行编写的二叉树, 如果每次添加的数都比之前所有的数要大, 比如把一个升序数组放入二叉树中, 二叉树其实并没有分叉, 因为每个节点都会挂在下一个节点的右节点上, 此时的二叉树退化成了一个链表.
链表里搜东西可就恐怖了, 至少都是O(n)的复杂度, 逆序添加也是一样的. 如果出现这种情况, 二叉树就失去意义了.
但是二叉查找树有一个很好的特点, 就是可以旋转, 也就是改变根节点, 由于其特点, 改变根节点之后, 还不会影响排序, 这就很有意思了. 当然, 旋转操作也不是很容易的, 来看看吧.
- AVL树和概念
- 平衡二叉查找树的实现
- 平衡二叉查找树的实现 - add方法
- 平衡二叉查找树的实现 - remove方法
- 测试
AVL树和概念
AVL树是可以保持平衡的二叉树, 所谓平衡, 指的是二叉树的任意节点, 其左子树和右子树的高度相差<=1.
来看一下四种旋转:
单旋转 - 右旋转
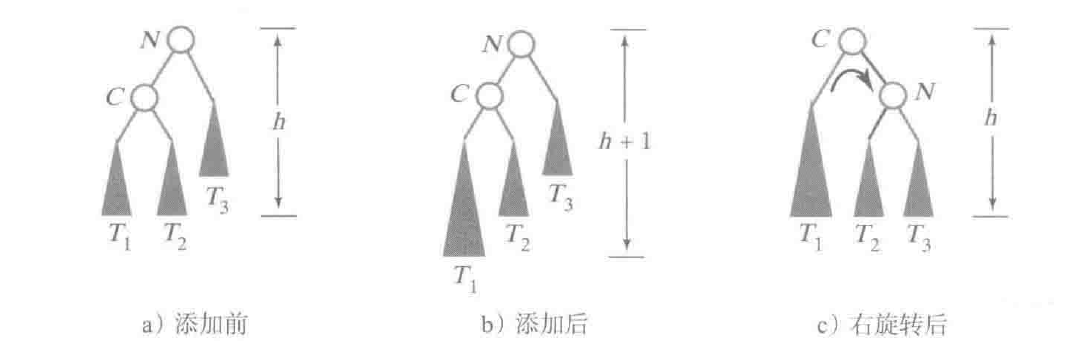这个旋转是在T1中添加一个叶子节点, 然后导致不平衡, 由于二叉树的特点, T2中的所有数值都大于C但是小于N, 所以就把C当成新节点, 然后把T2挂到N上去, 旋转之后就平衡了.
如果要写旋转代码的话, 就必须写一个能够返回旋转后的树的根节点的代码, 这样才能让N的父节点重新指向旋转之后的根节点, 所以方法的伪代码应该是:
public rotateRight(nodeN){
//获取T2树的引用和节点c的引用
NodeC = nodeN.getLeftChild()
T2 = NodeC.getRightChild()
//重新调整节点的关系
nodeN.leftChild = T2
nodeC.rightChild = nodeN
return nodeC
}
这样操作之后, 就是一个局部的旋转, 并返回此时的根节点NodeC, 如果需要的话拼到上一层节点上就可以了.
单旋转 - 左旋转
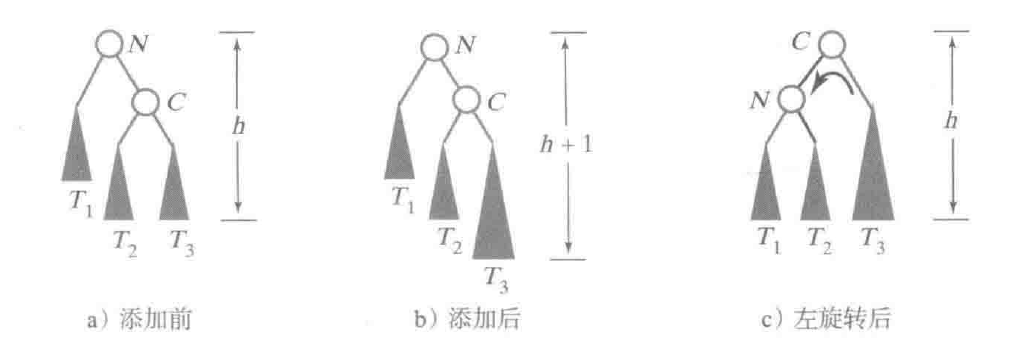左旋转和右旋转很像, 只不过是方向变了一下, 伪代码如下:
public rotateRight(nodeN){
//获取T2树的引用和节点c的引用
NodeC = nodeN.getRightChild()
T2 = NodeC.getLeftChild()
//重新调整节点的关系
nodeN.rightChild = T2
nodeC.leftChild = nodeN
return nodeC
}
可能已经发现了命名的规则, 哪一侧长, 这个旋转就叫做往另外一侧旋转, 比如右旋转中, 是左边的T1长了, 所以要往右旋转.
观察上边两个旋转, 要么在C是左节点的时候在C的左节点添加, 要么在C是右节点的时候在C的右节点添加.可见是在T1或者T3中添加, 如果在T2中添加会怎么样呢.
右 - 左旋转
以左旋转的初始状态为例, 如果此时给T2添加了一个元素, 应该如何操作呢. 注意观察节点C, 此时节点C是一个不平衡节点, 左边长, 很显然以C为根先右旋转一次.
旋转之后, T3会变长一截, 此时从NodeN的角度来说, 又是右比左长, 于是再以N为根节点, 进行一次左旋转, 旋转之后就得到了新的平衡树, 这就是右-左旋转.
这种情况的一般情形如下:
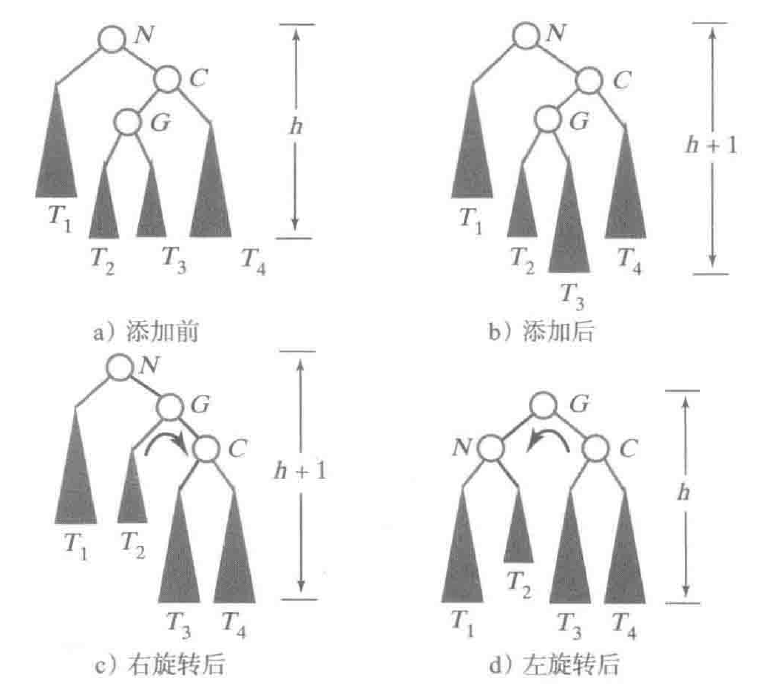可以看到, 实际的操作是先对C进行右旋转, 再对N进行左旋转, 即可得到结果. 写成伪代码就是:
public rotateRightLeft(nodeN){
//先右旋转nodeN的右节点C
rotateRight(nodeN.rightChild)
//再左旋转nodeN, 返回新节点
return rotateLeft(nodeN)
}
左 - 右旋转
这个也很好理解了, 其实也就是在右旋转的初始状态上往T2上添加数据, 先左旋转C, 再右旋转高一层的N就可以了. 伪代码如下:
public rotateLeftRight(nodeN){
//先左旋转nodeN的左节点C
rotateLeft(nodeN.leftChild)
//再右旋转nodeN, 返回新节点
return rotateRight(nodeN)
}
这样, 无论一个新节点添加在哪里, 都会落到这四种情况上去, 除非新节点直接挂在老节点下边.
可见, 这些平衡方法都是使用在添加(或者删除之后), 所以不需要更改接口, 来强化一下原来的二叉查找树就可以了.
这四种情况其实就是N是不是平衡和C是不是平衡的四种判断, 因此最终可以把这四种方法写到一起, 组成一个针对某个节点重新平衡的方法, 伪代码如下:
rebalance(nodeN) {
if(nodeN 的左子树长度 - 右子树长度 > 1) {
if(node.leftChild 的左子树长度 - 右子树长度 > 0){
//进到这个分支相当于右旋转的情况
rotateRight(nodeN)
} else {
//进到这个分支相当于在右旋转的初始状态下在T2添加过了数据, 所以是左-右旋转
rotateLeftRight(nodeN)
}
}else {
if(node.right 的右子树长度 - 左子树长度 > 1){
//进到这个分支相当于左旋转的情况
rotateLeft(nodeN)
} else {
//进到这个分支相当于在左旋转的初始状态下在T2添加过了数据, 所以是右-左旋转
rotateRightLeft(nodeN)
}
}
}
很显然, 搭配上在BinaryNode类中实现的getHeight()方法, 就可以在每次添加之后来进行旋转. 现在就可以来实现一下了.
平衡二叉查找树的实现 - 辅助函数编写
为了简便, 也不搞什么继承了, 就把BinarySearchTree复制一份起个名字, 然后先来编写一系列的旋转辅助方法, 先是左和右旋转:
public class AVLBinarySearchTree<T extends Comparable<? super T>> implements BinarySearchTreeInterface<T> {
......
private BinaryNode<T> rotateLeft(BinaryNode<T> nodeN) {
BinaryNode<T> nodeC = nodeN.getRightNode();
BinaryNode<T> T2 = nodeC.getLeftNode();
nodeN.setRightNode(T2);
nodeC.setLeftNode(nodeN);
return nodeC;
}
private BinaryNode<T> rotateRight(BinaryNode<T> nodeN) {
BinaryNode<T> nodeC = nodeN.getLeftNode();
BinaryNode<T> T2 = nodeC.getRightNode();
nodeN.setLeftNode(T2);
nodeC.setRightNode(nodeN);
return nodeC;
}
}
可以看到为了和伪代码一致, 可以把变量名都起成一样. 然后是左-右和右-左旋转:
private BinaryNode<T> rotateLeftRight(BinaryNode<T> nodeN) {
nodeN.setLeftNode(rotateLeft(nodeN.getLeftNode()));
return rotateRight(nodeN);
}
private BinaryNode<T> rotateRightLeft(BinaryNode<T> nodeN) {
nodeN.setRightNode(rotateRight(nodeN.getRightNode()));
return rotateLeft(nodeN);
}
这两个方法一定要记住要重新设置右节点, 否则就断开了. 逻辑在伪代码中已经非常清晰了.
最后把核心的rebalance方法写出来:
private BinaryNode<T> rebalance(BinaryNode<T> nodeN) {
int heightDifferent = getHeightDifferent(nodeN);
//左边比右边高超过1
if (heightDifferent > 1) {
//左边还比右边高, 右旋转
if (getHeightDifferent(nodeN.getLeftNode()) > 0) {
nodeN = rotateRight(nodeN);
//右边比左边高, 左-右旋转
} else {
nodeN = rotateLeftRight(nodeN);
}
//右边比左边高超过1
}else if (heightDifferent < -1) {
//右边还比左边高, 是左旋转
if (getHeightDifferent(nodeN.getRightNode()) < 0) {
nodeN = rotateLeft(nodeN);
//左边比右边高, 右-左旋转
} else {
nodeN = rotateRightLeft(nodeN);
}
}
return nodeN;
}
然后只需要编写一个辅助函数, 用来返回高度差即可:
private int getHeightDifferent(BinaryNode<T> nodeN) {
int leftHeight;
int rightHeight;
leftHeight = nodeN.getLeftNode() == null ? 0 : nodeN.getLeftNode().getHeight();
rightHeight = nodeN.getRightNode() == null ? 0 : nodeN.getRightNode().getHeight();
return leftHeight - rightHeight;
}
平衡二叉查找树的实现 - add方法
有了上边这些辅助方法后, 我们要做的就是在每次二叉树中新增和删除元素的时候, 接着就检测是否平衡并且进行调整. 考虑到上边这些方法都返回一个平衡后的子树的根节点, 很自然的想到可以使用递归的add方法来进行修改.
先是公共方法, 添加完成之后会检查一次是否平衡.
@Override
public T add(T newEntry) {
if (isEmpty()) {
root = new BinaryNode<>(newEntry);
return newEntry;
} else{
T result = add(newEntry);
root = rebalance(root);
return result;
}
}
然后是私有的递归方法, 每次添加之后, 都会立刻检查是否平衡:
private T add(T newEntry, BinaryNode<T> node) {
if (newEntry.compareTo(node.getData()) == 0) {
T result = node.getData();
node.setData(newEntry);
return result;
} else if (newEntry.compareTo(node.getData()) < 0) {
//左节点不为空意味这要在左子树中挂新玩意, 所以在添加之后, 立刻重平衡左节点
if (node.getLeftNode() != null) {
T result = add(newEntry, node.getLeftNode());
//添加完之后立刻平衡左节点
node.setLeftNode(rebalance(node.getLeftNode()));
return result;
//为null的情况新挂一个节点一定不会影响当前节点平衡
} else {
node.setLeftNode(new BinaryNode<>(newEntry));
return newEntry;
}
} else {
//另外一侧也是同样处理
if (node.getRightNode() != null) {
T result = add(newEntry, node.getRightNode());
node.setRightNode(rebalance(node.getRightNode()));
return result;
} else {
node.setRightNode(new BinaryNode<>(newEntry));
return newEntry;
}
}
}
平衡二叉查找树的实现 - remove方法
remove的修改也和add类似, remove本来就是返回删除后的节点, 只要在删除之后返回平衡后的节点就可以, 先修改公有方法:
public T remove(T entry) {
ReturnObject oldEntry = new ReturnObject(null);
BinaryNode<T> newRoot = removeEntry(getRootNode(), entry, oldEntry);
setRootNode(rebalance(newRoot));
return oldEntry.get();
}
公有方法中在获取最后的根节点的时候, 先将其重新平衡一次. 然后是私有方法:
private BinaryNode<T> removeEntry(BinaryNode<T> rootNode, T entry, ReturnObject oldEntry) {
if (rootNode != null) {
T rootData = rootNode.getData();
int comparison = entry.compareTo(rootData);
if (comparison == 0) {
oldEntry.setEntry(rootData);
rootNode = removeFromRoot(rootNode);
} else if (comparison < 0) {
BinaryNode<T> leftChild = rootNode.getLeftNode();
BinaryNode<T> subtreeRoot = removeEntry(leftChild, entry, oldEntry);
rootNode.setLeftNode(subtreeRoot);
} else {
BinaryNode<T> rightChild = rootNode.getRightNode();
rootNode.setRightNode(removeEntry(rightChild, entry, oldEntry));
}
if (rootNode != null) {
rootNode = rebalance(rootNode);
}
}
return rootNode;
}
很显然, 只要在每次处理完成之后, 返回之前, 重新平衡一次rootNode就可以了.这里要注意的是子树很可能被删光, 所以要判断节点是不是为null, 为null则无需平衡.
这样就编写好了每次在插入和删除之后进行平衡的二叉树, 这里还可以改进的地方是每次计算高度都需要使用递归, 可以在每个节点中包含高度, 不过实现起来更加复杂一些.
测试
可以写代码来测试一下, 还记得我们在二叉树中用过一个findNode私有方法, 将其改成公有, 然后我们来查找一个二叉树某一个节点的父元素就可以了:
public static void main(String[] args) {
int data[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
BinarySearchTree<Integer> noBalanceTree = new BinarySearchTree<>();
for (Integer s : data) {
noBalanceTree.add(s);
}
for (Integer s : data) {
System.out.println(noBalanceTree.findNode(s));
}
AVLBinarySearchTree<Integer> balanceTree = new AVLBinarySearchTree<>();
for (Integer s : data) {
balanceTree.add(s);
}
for (Integer s : data) {
System.out.println(balanceTree.findNode(s));
}
}
noBalanceTree的结果如下:
NodePair{targetNode=BinaryNode{data=1}, fatherNode=null}
NodePair{targetNode=BinaryNode{data=2}, fatherNode=BinaryNode{data=1}}
NodePair{targetNode=BinaryNode{data=3}, fatherNode=BinaryNode{data=2}}
NodePair{targetNode=BinaryNode{data=4}, fatherNode=BinaryNode{data=3}}
NodePair{targetNode=BinaryNode{data=5}, fatherNode=BinaryNode{data=4}}
NodePair{targetNode=BinaryNode{data=6}, fatherNode=BinaryNode{data=5}}
NodePair{targetNode=BinaryNode{data=7}, fatherNode=BinaryNode{data=6}}
NodePair{targetNode=BinaryNode{data=8}, fatherNode=BinaryNode{data=7}}
NodePair{targetNode=BinaryNode{data=9}, fatherNode=BinaryNode{data=8}}
NodePair{targetNode=BinaryNode{data=10}, fatherNode=BinaryNode{data=9}}
NodePair{targetNode=BinaryNode{data=11}, fatherNode=BinaryNode{data=10}}
NodePair{targetNode=BinaryNode{data=12}, fatherNode=BinaryNode{data=11}}
NodePair{targetNode=BinaryNode{data=13}, fatherNode=BinaryNode{data=12}}
NodePair{targetNode=BinaryNode{data=14}, fatherNode=BinaryNode{data=13}}
NodePair{targetNode=BinaryNode{data=15}, fatherNode=BinaryNode{data=14}}
NodePair{targetNode=BinaryNode{data=16}, fatherNode=BinaryNode{data=15}}
很显然noBalanceTree退化成了链表.
balanceTree的结果如下:
NodePair{targetNode=BinaryNode{data=1}, fatherNode=BinaryNode{data=2}}
NodePair{targetNode=BinaryNode{data=2}, fatherNode=BinaryNode{data=4}}
NodePair{targetNode=BinaryNode{data=3}, fatherNode=BinaryNode{data=2}}
NodePair{targetNode=BinaryNode{data=4}, fatherNode=BinaryNode{data=8}}
NodePair{targetNode=BinaryNode{data=5}, fatherNode=BinaryNode{data=6}}
NodePair{targetNode=BinaryNode{data=6}, fatherNode=BinaryNode{data=4}}
NodePair{targetNode=BinaryNode{data=7}, fatherNode=BinaryNode{data=6}}
NodePair{targetNode=BinaryNode{data=8}, fatherNode=null}
NodePair{targetNode=BinaryNode{data=9}, fatherNode=BinaryNode{data=10}}
NodePair{targetNode=BinaryNode{data=10}, fatherNode=BinaryNode{data=12}}
NodePair{targetNode=BinaryNode{data=11}, fatherNode=BinaryNode{data=10}}
NodePair{targetNode=BinaryNode{data=12}, fatherNode=BinaryNode{data=8}}
NodePair{targetNode=BinaryNode{data=13}, fatherNode=BinaryNode{data=14}}
NodePair{targetNode=BinaryNode{data=14}, fatherNode=BinaryNode{data=12}}
NodePair{targetNode=BinaryNode{data=15}, fatherNode=BinaryNode{data=14}}
NodePair{targetNode=BinaryNode{data=16}, fatherNode=BinaryNode{data=15}}
从结果可以发现, 添加到16个元素的时候, 现在的根节点是8, 将这个二叉树画出来就是:
8
/ \
4 12
/ \ / \
2 6 10 14
/ \ / \ / \ / \
1 3 5 7 9 11 13 15
\
16
然后来删除几项, 比如 9, 10, 11 ,让树局部变得不平衡:
balanceTree.remove(9);
balanceTree.remove(10);
balanceTree.remove(11);
for (Integer s : data) {
System.out.println(balanceTree.findNode(s));
}
结果是:
NodePair{targetNode=BinaryNode{data=1}, fatherNode=BinaryNode{data=2}}
NodePair{targetNode=BinaryNode{data=2}, fatherNode=BinaryNode{data=4}}
NodePair{targetNode=BinaryNode{data=3}, fatherNode=BinaryNode{data=2}}
NodePair{targetNode=BinaryNode{data=4}, fatherNode=BinaryNode{data=8}}
NodePair{targetNode=BinaryNode{data=5}, fatherNode=BinaryNode{data=6}}
NodePair{targetNode=BinaryNode{data=6}, fatherNode=BinaryNode{data=4}}
NodePair{targetNode=BinaryNode{data=7}, fatherNode=BinaryNode{data=6}}
NodePair{targetNode=BinaryNode{data=8}, fatherNode=null}
NodePair{targetNode=null, fatherNode=null}
NodePair{targetNode=null, fatherNode=null}
NodePair{targetNode=null, fatherNode=null}
NodePair{targetNode=BinaryNode{data=12}, fatherNode=BinaryNode{data=14}}
NodePair{targetNode=BinaryNode{data=13}, fatherNode=BinaryNode{data=12}}
NodePair{targetNode=BinaryNode{data=14}, fatherNode=BinaryNode{data=8}}
NodePair{targetNode=BinaryNode{data=15}, fatherNode=BinaryNode{data=14}}
NodePair{targetNode=BinaryNode{data=16}, fatherNode=BinaryNode{data=15}}
很显然9, 10, 11 找不到了, 把现在的树画一下看看:
8
/ \
4 14
/ \ / \
2 6 12 15
/ \ / \ \ \
1 3 5 7 13 16
真的是神奇啊. 后边的2-3树和2-4树还有红黑树就好好看看理论吧....
Java中的红黑树的实现主要是包含在其他结构中, HashMap使用的是数组, 数组每一个元素是红黑树. TreeMap<K,V>则是直接使用红黑树存放每一个键值对. SortedMap内部也是利用TreeMap的实现. 红黑树所有的操作都是O(logN)的, 已经相当快了.
